Prologue
This article describes why and how I wrote absolut; a Rust crate for automating a common pattern of constructing SIMD byte-wise lookup tables. I learned about this technique while studying the Parsing Gigabytes of JSON per Second paper by Geoff Langdale & Daniel Lemire.
The TBL instruction
The centerpiece of SIMD lookup tables is the PSHUFB instruction on x86 or the TBL instruction on ARM. For the remainder of the article, I will use the latter in code examples1.
I use conventional array indexing notation to refer to the individual bytes of a
vector register, e.g. reg[n] denotes the nth byte of the register
reg. Moreover, for any byte value b (i.e. an unsigned integer in the range
0..256) I define lo(b) = b & 0xF and hi(b) = b >> 4 which correspond,
respectively, to the four least significant bits (i.e. low nibble), and the four
most significant bits of b (i.e. high nibble).
The tbl instruction operates on three 128-bit vector registers which I
henceforth denote as dst, src and tlo2. dst is an output register, while
src and tlo are input registers.
Having established sufficiently expressive syntax, we can specify the behavior
of tbl as follows; the nth byte of dst is the result of indexing tlo using
the low nibble of the nth byte of src. However, if nth byte of src is greater
than 16, then the nth byte of dst is zero.
More precisely, if 0 <= src[n] < 16, then dst[n] = tlo[lo(src[n])] otherwise dst[n] = 0; for any n in the range
0..16. Notice that this is well defined since lo(b) is always within the
range 0..16.
From nibbles to bytes
The downside of the tbl instruction is that it maps nibbles to bytes and not
bytes to bytes. Therefore, constructing a bytewise lookup table would require
more machinery.
To get around one could perform two tbl instructions; the first one operates
on the low nibbles of src using a tlo table, while the second one operates
on the high nibbles of src using a thi table (by shifting every byte of
src to right by 4 bits)2.
Next, the two resulting vector registers should be combined in one way or
another. It turns out that a logical AND operation is particularly useful
here3. Assuming a careful choice of the two register tables, one can perform
a bytewise lookup using only three instructions.
The bytewise lookup table we seek can be written as lut(b) = tlo[lo(b)] & thi[hi(b)]. Consequently, solving for lut is equivalent to
solving for tlo and thi.
SMT for the rescue
 |
|---|
The lookup table used in simdjson |
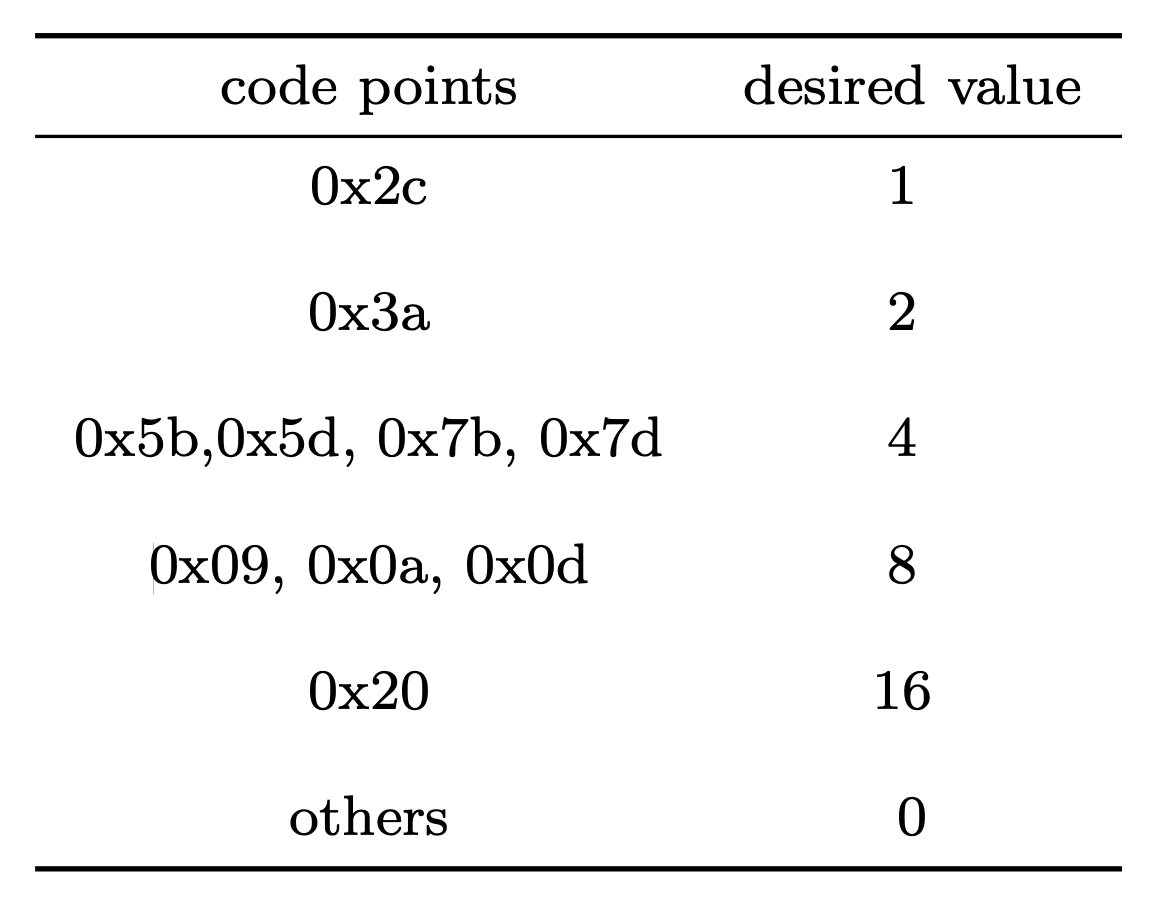
At first glance, it is not at all obvious to compute tlo and thi given a
desired byte mapping. Since any solution would need to satisfy the following
constraints:
lut(0x2C) == 1
lut(0x3A) == 2
lut(0x5B) == 4
lut(0x5D) == 4
lut(0x7B) == 4
lut(0x7D) == 4
lut(0x09) == 8
lut(0x0A) == 8
lut(0x0D) == 16
lut(0x20) == 16
lut(_) == 0
Where _ is a placeholder for all other bytes, which conceptually expands the
list of constraints into exactly 256 items. I'm not doing this by hand4
Fortunately, an SMT solver is perfect for such a task. Put another way, our problem can be neatly described as an SMT problem.
The SMT problem is beyond the scope of this article. For our purposes, an SMT solver such as Z3 is a black box that takes a set of constraints and either finds a solution, proves that there is no possible solution, or fails to decide either way.
Z3 has a built-in understanding of bit-vectors, arrays and functions. Consequently, the constraints described above can be passed to it with little transformation.
All that's left is to write a makeshift Python script to call Z3 and solve for any lookup table we might need. Right?
Introducing absolut
The structure of simdjson is not particularly oriented towards reuse. A helpful set of transformations would be to break it into smaller, reusable components without compromising performance. Particularly egregious is the use of many hard-coded tables for the VPSHUFB-based character matcher; not only does this hard code the particular characters and character classes, it cannot be reused in a situation as-is in a number of situations (e.g. overly numerous character classes or ones where a desired character class includes one with the high bit set).
— Geoff Langdale, from https://branchfree.org/2019/02/25/paper-parsing-gigabytes-of-json-per-second
There is no reason why the process of generating constraints and solving them could not be automated even further; through a compiler plugin which would lift it from a side tool to something akin to a language feature.
absolut is meant to be such a compiler plugin.
Rust is suitable for implementing this, thanks to its strong meta-programming
capabilities. Unfortunately, this is precisely where I got bogged down the most
while writing absolut.
Having never written a procedural macro before, I was unsure whether I should use a function-like macro, a derive macro, or an attribute macro. However, it was easy to eliminate the macros-by-example choice since that would mean shoving all of Z3 into client code.
A Function-like procedural macro
I implemented my first prototype of absolut as a function-like macro which
looked something like the following:
let SimdTable { lo, hi } = simd_table! {
b',' => 1,
b':' => 2,
b'[' | b']' | b'{' | b'}' => 4,
b'\t' | b'\n' | b'\r' => 8,
b' ' => 16,
_ => 0
};
struct SimdTable {
/// Low nibble table.
lo: [u8; 16],
/// High nibble table.
hi: [u8; 16],
}
I believe that the syntax of a procedural macro should be natural; meaning
that it should closely mimic proper Rust syntax as much as
possible. simd_table! { .. } fits this description reasonably well, as it
looks almost like a match expression. However, this syntax quickly fell apart.
First, it turns out one needn't hard-code the value each byte is mapped to, i.e. its class. The class of a byte can simply be a free variable that the SMT solver will solve for. This is not simply more convenient to use but also allows for the solver to explore every possible solution. To achieve this, one could simply replace integer literals with identifiers in each match arm.
let SimdTable { lo, hi } = simd_table! {
b',' => comma,
b':' => colon,
b'[' | b']' | b'{' | b'}' => brackets,
b'\t' | b'\n' | b'\r' => control,
b' ' => space,
_ => 0
};
This is quite problematic as it implicitly creates several bindings without
ascertaining where they would be stored. Should comma be a field of
SimdTable? No, that would require us to transparently generate a new type for
every usage of simd_table. I don't see a good answer here.
Furthermore, it would be useful to customize the length of lo and hi as
tbl supports tables of size 16, 32, 48 or, 64, for instance. Where should this
optional argument be put? It's not clear to me how this could be done without
sacrificing the naturalness of the syntax.
An attribute procedural macro
After a few days of bikeshedding, it became clear to me that simd_table should
be an attribute macro that implements a SimdTable<LANES> trait on an enum;
each variant of which would represent a class.
All variants would accept an attribute specifying which bytes belong to the class they signify. Moreover, the discriminant of each variant would be the value of its corresponding class.
#[simd_table(LANES = 16)]
enum JsonSimdTable {
#[matches(b',')]
Comma,
#[matches(b':')]
Colon,
// b']' breaks my syntax highlighter :/
#[matches(b'{' | b'}' | b'[' | 0x5D)]
Brackets,
#[matches(b'\t' | b'\r' | b'\n')]
Control,
#[matches(b' ')]
Space,
// Match all other bytes
#[wildcard]
Other = 0,
}
trait SimdTable<LANES> {
/// Low nibble table.
const LO: [u8; LANES];
/// High nibble table.
const HI: [u8; LANES];
}
Note that since absolut needs to rewrite the discriminant of all variants, one
cannot implement this version of simd_table as a derive macro.
The classic use case
A usage scenario of absolut would be scanning a byte array for characters of
interest, as is done in simdjson. Usage of the tbl instruction requires
architecture-specific intrinsic functions.
let input = b"\"o\":{\"k\":[1,2]}\n";
// vld1q_u8: Load 1 Quadword (128-bit) Vector
// of unsigned bytes from memory
let v_input = vld1q_u8(input.as_ptr());
let v_table_lo = vld1q_u8(JsonSimdTable::LO.as_ptr());
let v_table_hi = vld1q_u8(JsonSimdTable::HI.as_ptr());
// vdupq_n_u8: DUPlicate an unsigned byte scalar
// to create a Quardword Vector
let v_mask = vdupq_n_u8(0b1111);
// vandq_u8: compute a bitwise AND of two Quardword
// Vectors of unsigned byte
let v_input_lo = vandq_u8(v_input, v_mask);
// vshrq_n_u8: SHift Right all unsigned bytes of
// a Quardword Vector by a const amount
let v_input_hi = vshrq_n_u8::<4>(v_input);
// vqtbl1q_u8: perform a TBL lookup using 1 Quardword
// Vector table of unsigned bytes on a Quardword Vector
let v_lookup_lo = vqtbl1q_u8(v_table_lo, v_input_lo);
let v_lookup_hi = vqtbl1q_u8(v_table_hi, v_input_hi);
let v_lookup = vandq_u8(v_lookup_lo, v_lookup_hi);
let mut lookup = [0; 16];
vst1q_u8(lookup.as_mut_ptr(), v_lookup);
In the code example above, we use the JsonSimdTable declared earlier to scan
the JSON string "o":{"k":[1,2]}\n for commas, colons, brackets, and control
characters5. This results in a lookup array with the same length as input,
but with each input byte replaced with its class value.
assert_eq!(
lookup,
[
Other as u8, // "
Other as u8, // o
Other as u8, // "
Colon as u8, // :
Brackets as u8, // {
Other as u8, // "
Other as u8, // k
Other as u8, // "
Colon as u8, // :
Brackets as u8, // [
Other as u8, // 1
Comma as u8, // ,
Other as u8, // 2
Brackets as u8, // ]
Brackets as u8, // }
Control as u8 // \n
]
);
Further work
The current implementation of absolut is quite incomplete. For instance, the
x86 vpshufb instruction mentioned at the beginning of the article behaves
quite differently from the ARM tbl instruction: bytes are unconditionally
mapped to zero when their most significant bit is set and not when they
exceed 16.
This is important because all tables on x86 have a length of 16. 256-bit and
512-bit versions of vpshufb simply perform respectively two and four 16-byte
table lookups in parallel6. Right now, absolut only works in the common case of
16-byte tables.
Furthermore, I experienced significantly long compile times for the Z3 solver
while testing absolut. This might be a non-issue as it only needs to be
compiled once as an external dependency.
Still, I can't help but wonder if absolut could benefit from a hand-rolled
small SMT solver specifically designed for its specific purposes. However, this
"embedded" solver would need to perform reasonably well. Trading slow
compilation for slow runtime in absolut is a bad bargain.
Lastly, in keeping with tradition,absolut currently has zero documentation,
except for this article. Granted, the crate itself only exports two items: the
simd_table macro and the SimdTable trait.
However, the simd_table macro will eventually accept many more arguments to
support more usage scenarios. Correctly documenting the interactions between
these arguments will be challenging. absolut will also need useful error
messages to explain invalid user configurations.
Epilogue
If you happen to be a byte-bashing wizard, please do not hesitate to point out
use cases where absolut falls short. And if you are an experienced rustacean
with reservations on how absolut is implemented, I would love to hear them
out. Issues and
PRs are welcome. Even an
old-fashioned email would be greatly appreciated.
I'm no evangelist, I just happen to be writing this on an ARM machine.
tlo stands for "Table LOw" while thi stands for "Table HIgh".
It might be fruitful to explore other operations here, such as XOR.
I have to admit I am particularly bad with manual computations, perhaps this is why I gravitate towards computers.
This is incompatible with the behavior of ARM mentioned earlier.
If you're curious as to why this is useful, I encourage you to read the simdjson paper yourself!